![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
15 Cards in this Set
- Front
- Back
|
Solve for x. x+2=20
|
x=18
|
|
|
Solve for r. 20 = 2(r+7)
|
r=3
|
|
|
Solve for y. -35= 5(y-2)
|
y=-5
|
|
|
Does this equation have a positive solution, negative solution, zero solution or no solution? (Determine without solving). 7-5w=3
|
The equation has a positive solution.
|
|
|
Does this equation have a positive solution, negative solution, zero solution or no solution? (Determine without solving). 4a=9a
|
The solution is zero.
|
|
|
Does this equation have a positive solution, negative solution, zero solution or no solution? (Determine without solving). y=y+1
|
There is no solution.
|
|
|
You have a coupon worth $18 off the purchase of a scientific calculator. At the same time, the calculator is offered with a discount of 15%, but no further discounts may be applied. For what tag price on the calculator do you pay the same amount for each discount?
|
p=tag price (dollars)
p-18=0.85p p-0.85p=18 0.15p=18 p=120 You pay the same for each discount when the tag price is $120. |
|
|
Solve for y=7. y= (4/3)x - 7
|
x=10 1/2
|
|
|
solve for y = 4. y= (3/2)x-9
|
x= 8 2/3
|
|
|
Solve for x. 9(x+10) = x-22
|
x= -14
|
|
|
The solution to a system of two linear equations can be found algebraically or by graphing. On a graph, the solution is the point at which the two lines __________.
|
The solution to a system of two linear equations can be found algebraically or by graphing. On a graph, the solution is the point at which the two lines intersect.
|
|
|
Consider the linear equation 5x-2y=3. Find a second linear equation to create a system of equations that has exactly 1 solution.
|
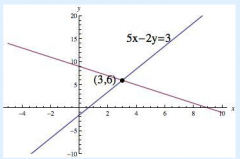
Step 1: Graph the line 5x-2y=3.
Step 2: Find a point on the line 5x-2y=3 and create another line that also contains that point, but is not the same line. (student may choose any point on the line, for this example I chose (3,6)). Step 3: find values for a, b, or c in the equation ax+by=c that work with x=3 and y=6 (the point that I chose) but are not the same values as the ones in the given equation. If we choose a=1 and b=1, then x+y=c 3+6=c 9=c. Step 4: This means that (3,6) is a solution to the equation x+y=9 and a solution to the equation 5x-2y=3, so the system of equations is: 5x-2y=3 x+y=9 |
|
|
You are a representative for a cell phone company and it is your job to promote different cell phone plans. Your boss asks you to visually display 3 plans and compare them so you can point out the advantages of each plan to your customers. Plan A costs a basic fee of $29.95 per month plus 10 cents per text message. Plan B costs a basic fee of $49.95 per month and 5 cents per text message. Plan C costs a basic fee of $90.20 per month and has unlimited text messages. Create a graph to show the price of each plan per month based on the number of text messages sent.
|
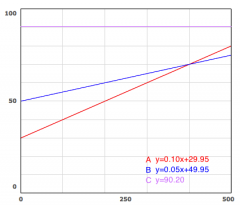
|
|
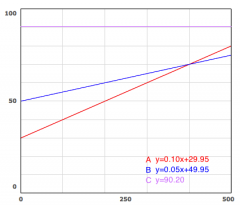
Which of the plans A, B, or C will save you the most money if you send 500 text messages per month? 0 text messages? 100 text messages?
|
If you send 500 text messages a month, plan B will save the most money. If you send 0 text messages, plan A will save the most money, and if you send 500 text messages, plan B will save you the most money.
|
|
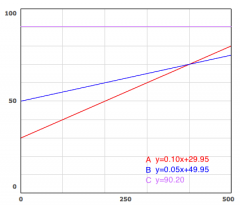
Estimate how many text messages you would have to send per month for plan C to be the most cost efficient plan.
|
You would have to send more than 603 text messages for plan C to be the most cost efficient.
|

