Chapter 2 - Describing Location In A Distribution

Front 1

Standardizing

Back 1

The process of converting original values to standard deviation units.

Front 2

Standardized Value

Back 2

Hint 2

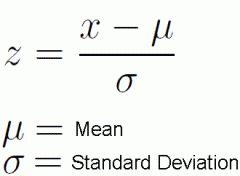
Synonymous with the z-score.

Front 3

Z-score

Back 3

The z-score is synonymous with the standardized value.

Front 4

Percentile

Back 4

The pth percentile of a distribution is the value with with p percent of observations below it.

Front 5

Chebyshev's inequality

Back 5

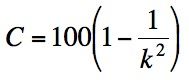
In any distribution, the percent of observations falling within k standard deviations of the mean is at least C.

Front 6

Mathematical Model

Back 6

It is the description of a system using mathematical concepts and language.
or
A mathematical representation of a process, device, or concept by means of a number of variables which are defined to represent the inputs, outputs, and internal states of the device or process, and a set of equations and inequalities describing the interaction of these variables.

Front 7

Density Curve

Back 7

It is a curve that:

- always on or above the horizontal axis, and
- has area exactly 1 underneath it.

A density curve describes the overall pattern of a distribution. The area under the curve and above any interval of values on the horizontal axis is the proportion of all observations that fall in that interval.

Hint 7

Front 8

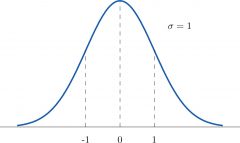
Normal Curve

Back 8

A symmetrical curve representing the normal distribution.

Hint 8

Front 9

Median of a Density Curve

Back 9

This is the "equal-areas point," the point that divides the area under the curve in half.

Hint 9

Front 10

Mean of a Density Curve

Back 10

It is the " balance point," at which the curve would balance if made of solid material.

Hint 10

Front 11

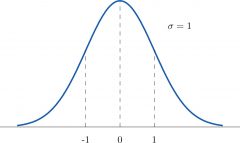
Standard Deviation of a Density Curve

Back 11

Represented by the greek letter small sigma.

Hint 11

Front 12

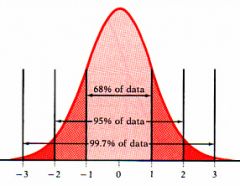
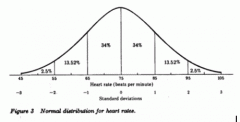
The 68-95-99.7 Rule

Back 12

In the Normal distribution with mean mu and standard deviation sigma:
-Approximately 68% of the observations fall within one standard deviation of the mean.
-Approximately 95% of the observations fall within 2 standard deviations of the mean.
-Approximately 99.7% of the observations fall within 3 standard deviations of the mean.

Hint 12

Front 13

Standard Normal Distribution

Back 13

It is the Normal distribution N(0,1) with mean 0 and standard deviation 1.

Hint 13

Front 14

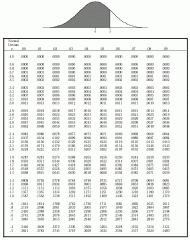
Standard Normal table

Back 14

a table of areas under the standard normal curve. Each table entry = area to left of z

Hint 14

Front 15

Steps to Solving Normal Distributions

Back 15

1. State the problem
2. Standardize and draw picture
3. Use the table
4. Conclusion

Hint 15

Front 16

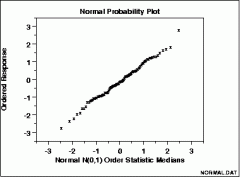
Normal Probability Plot

Back 16

If points lie close to a straight line then the plot shows that data is Normal. Deviations from a straight line display a non-Normal distribution.

Hint 16