![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
13 Cards in this Set
- Front
- Back
|
What is acceleration? |
Acceleration is the measure of how quickly something gets faster. |
|
|
How can acceleration be calculated? |
You can calculate the acceleration of an object from its change in velocity and the time taken. Velocity is not exactly the same as speed. Velocity has a direction as well as a speed. |
|
|
What formula is used to calculate acceleration? |

The equation for acceleration can also be represented as: a = (v-u) ÷ t a is acceleration in m/s/s or m/s^2 (^2 = power of 2) v is final velocity in m/s u is initial velocity in m/s t is time in s |
|
|
What is deceleration? |
Deceleration, or negative acceleration, is observed when an object slows down. The units are the same as for acceleration but the number has a negative symbol before it. |
|
|
What is the equation relating acceleration to force and mass? |
F = m × a F is the resultant force in newtons, N m is the mass of the object in kilograms, kg a is the acceleration of the object in metres per second squared, m/s/s (m/s^2) |
|
|
The mass of the rocket is 100 g and it goes from rest to 20 m/s in 0.5 s. What is the acceleration and accelerating force? |
a = (20 - 0) ÷ 0.5 = 40 m/s^2 F = 0.1 x 40 = 4 N |
|
|
The rocket then hits the wall and stops in 0.02 seconds. Calculate the deceleration of the rocket as it hits the wall. |
a = (0 - 20) ÷ 0.02 = -1000 m/s^2
It decelerates at a rate of 1 000 m/s^2. |
|
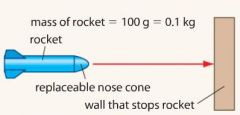
A student found that increasing the length of the disposable nose cone decreased the deceleration when the rocket in the Figure hit the wall. This stopped the rocket getting damaged so much. Use the relationship between force, mass and acceleration to suggest why this makes sense. |
The longer the nose cone, the longer the rocket takes to stop so deceleration is lower. This means that the force on the rocket is smaller so less damage is done, just like crumple zones in cars. |
|
|
The student repeated the toy rocket experiments with the rocket moving vertically. She found that accelerations were smaller. Explain why. |
Gravity acts against the rocket push so resultant force is smaller. |
|
|
The student then conducted experiments with the rocket over greater distances on playing fields. She found that the acceleration was not constant. Acceleration decreased as the rocket got faster. Why this might be? |
Air resistance increases as the rocket gets faster. At lower speeds this is not significant but at higher speeds the resultant force reduces. |
|
|
A force of 15 N pushes a ball with a mass of 3 kg. What is its acceleration? A force of 25 N is applied to a trolley. It accelerates at 2 m/s^2. What is its mass? |
a = 5 m/s2. m = 12.5 kg. |
|
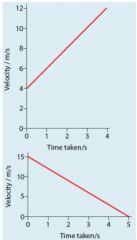
Calculate the acceleration for each of the graphs in the Figure. |
Top graph shows 2 m/s^2. Bottom graph shows –3 m/s^2. |
|
|
What are the key points to remember? |
Acceleration is change in velocity in a given time. Force= mass × acceleration, F = m × a. Acceleration can be calculated from the slope of a velocity-time graph. Measurements must be in the correct units for calculations. |

