![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
168 Cards in this Set
- Front
- Back
|
define crystal lattice |
Construcyed by infinite repetition of identical group of atoms (basis) |
|
|
define primative lattice cell |
a parallelogram with the axes of primative vectors |
|
|
define primative vectors |
for any two points r and r prime look the same |
|
|
how many atoms are in the 3 types of cubic lattice |
simple cubic = 1 atom BCC = 2 atoms FCC = 4 atoms |
|
|
translation vector |
T = U1a1 + u2a2 + u3a3 |
|
|
r prime |
r' = r + T |
|
|
distance between basis |
rj = xja1 + yja2 + zja3 |
|
|
r prime with a basis of 2 atoms |
r' = r + T + rj |
|
|
bands of an insulator |

|
|
|
bands of a semiconductor |

|
|
|
bands of a metal |

|
|
|
directions of r |
characterised by u, v, w that have the ratio of u1 u2 u3 |
|
|
planes of lattices |
defined by the intercepts of plane with crystal lattice. find the reciprocal and reduce the fractions to integers |
|
|
Fermi Dirac distribution |
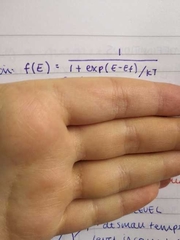
|
|
|
dispersion relationship |

|
|
|
total number of states inside a sphere |

|
|
|
Fermi k vector |

|
|
|
Fermi energy |

|
|
|
density of states |

|
|
|
momentum |

|
|
|
Fermi temperature |
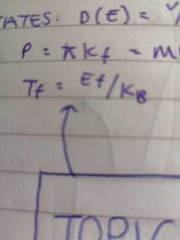
|
|
|
Fermi level at small temperatures |
Fermi level = Fermi energy |
|
|
proof that Y(x+L) = Y(x) |

|
|
|
principles of free electron model |
ignored crystal lattice valence electrons move almost freely through volume |
|
|
cons of free electron model |
fails to account for: metallic colour |
|
|
define scattering time tau |
time taken for an electrone velocity to relax to zero |
|
|
mobility mu |
a steady state electron velocity acquired in the electric field with a value of 1 V/m |
|
|
electron motion |

|
|
|
velocity in terms of scattering times |
v = - eEtau/m |
|
|
mobility |
v = - mu E mu = - e tau/m |
|
|
current density |
J = - nev = sigma E |
|
|
conductivity |
sigma = ne^2 tau/ m |
|
|
resistivity |
ro = 1/ne mu |
|
|
free mean path |
L = v tau |
|
|
drude model |
ignores ion cores and interactions. of electrons with periodic crystal lattice |
|
|
electrons in Fermi sphere in absense of E field |

|
|
|
electrons in Fermi sphere with application of E field |

|
|
|
phonon scattering |

|
|
|
defect scattering |
collisions are elastic scattering with large delta k causes resistance |
|
|
matthiesens rule |

|
|
|
Bragg diffraction |
2asin(theta) = N lamda |
|
|
reciprocal lattice vector |
G = 2pi/a = delta k |
|
|
group velocity |
vg = dw/dk = 1/h bar dE/dk |
|
|
electrons experiencing Bragg diffraction |
have a k vector of k = ±npi/a |
|
|
K vectir in 1st brouillion zone |
±pi/a |
|
|
when are standing waves formed in a 1D chain |
when K = ±pi/a |
|
|
positive and negative wavefunctions. of standing waves |
Y+ = 2cos(pix/a) Y- = 2isin(pix/a) |
|
|
probability of wavefunctions |
Y+*Y- piles up ON ions Y-*Y+ piles up INBETWEEN ions |
|
|
application of E field in a half filled Conduction band |
enables shift of electron distribution with respect to zero non zero current |
|
|
application of E field in a filled Conduction band |
current allows some electrons to jump the band gap |
|
|
overlapping bands |
energy of first state can be higher than that of the second so the states in second band are filled first |
|
|
efficient diffraction |
delta k = 2ksin(theta) |
|
|
Bragg plane |
perpendicular bisector planes that divide boundries of brouillion zones |
|
|
reduced zone schemes |
high order BZ are folded back into 1st BZ by changing k vectors by a multiple of G |
|
|
Construction of Bragg planes |
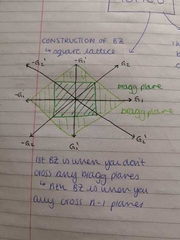
|
|
|
define Fermi surface |
surface of a sphere separating full and empty states in K space |
|
|
diagram of Fermi surface |
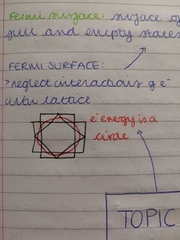
|
|
|
deformation of Fermi surface |

|
|
|
modification of Fermi surface rules |

|
|
|
how to measure Conduction band distribution of metals |

find Fermi energy by emission of xrays |
|
|
define tight binding model |
constructs electron bands and wavefunctions |
|
|
how does tight binding model work |

|
|
|
how are energy bands formed |
from different electron orbitals depending on the distance between atoms |
|
|
derivation of effective mass |

|
|
|
define a hole |
an electron with positive mass and change |
|
|
creation of a hole in a semiconductor |

|
|
|
do holes create current |
yes because they have positive charge |
|
|
how to make a semiconductor more conductive |
add elements to make more holes or higher electron concentration |
|
|
radius of an atom |
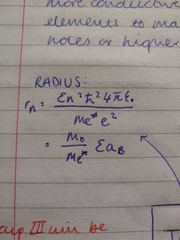
|
|
|
donors |

|
|
|
what group will be donors for group IV |
group V |
|
|
acceptors |

|
|
|
what group will be acceptors for group IV |
group III |
|
|
binging energy |

|
|
|
number of electrons |

|
|
|
electron/hole density |

|
|
|
dependance of Fermi level on temperature |

|
|
|
Fermi level. at low temperature |

|
|
|
concentration of electrons at low. temp |

|
|
|
entrinsic semiconductors |
doped semiconductors where electron concentrationd are given by dopants |
|
|
intrinsic material |
when Na = Nd then both will be ionised and no holes or electrons will be in bands |
|
|
types of semiconductor |

|
|
|
lorentz force |
F = - ev x B |
|
|
Hall electric field |

eEh=ev x B |
|
|
velocity in direction of Ex |
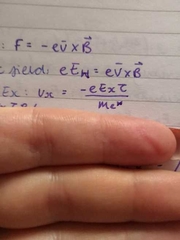
|
|
|
what direction is hall field. in |
Y direction |
|
|
Hall coefficient |
Rh = 1/ne = EyB/j |
|
|
current density in terms of width and thickness |
J = I/wt |
|
|
Hall velocity |
Vh=Ey w |
|
|
Hall effect with electrons and holes |

|
|
|
direction of electrons around B |
will move in anticlockwise direction |
|
|
cyclotron resonance |

|
|
|
absorption coefficient |

|
|
|
complex velocity |

|
|
|
circularly polarised E field |
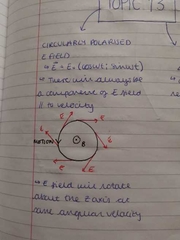
|
|
|
FWHM of cyclotron resonance |

|
|
|
define electrical conductivity |
depends on carrier concentration and their distribution of thermal velocities |
|
|
where is Fermi level |
somewhere in band gap |
|
|
kinetic energy of electrons in Conduction band |
1/2 mv^2 = 3/2 kT |
|
|
charge defects |

|
|
|
free mean path wrt T at low T |
proportional to T^2 |
|
|
scattering time with respect to T at low T |
tau is proportional to T^3/2 |
|
|
free mean path wrt T at high T |
proportional to T^-1 |
|
|
scattering time wrt T at high T |
proportional to T^-3/2 |
|
|
optical absorption |

|
|
|
what is an exciton |

|
|
|
moss-burstein effect |

|
|
|
derive dielectric function |

|
|
|
what happens when w>wp |
wave will propagate |
|
|
what happens when w<wp |
wave will be reflected |
|
|
electrons under electric field - electrostatic screening |

|
|
|
dielectric function of semiconductors |

|
|
|
dispersion relation wrt dielectric function |

|
|
|
define plasmon |
a quantum or longitudinal plasma oscillation |
|
|
plasma frequency |
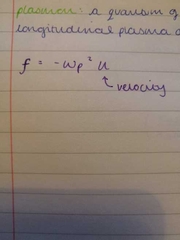
|
|
|
wp |
n^2/epsilon naught me* |
|
|
where is electronic paramagnetic found |
atoms, molecules and lattice defects with odd number of electrons free atoms and ions with partially. filled inner shell metals |
|
|
total angular momentum |
J = angular momentum + spin |
|
|
hunds rules |

|
|
|
magnetic dipole of orbital motion |

|
|
|
magnetic moment for spin |
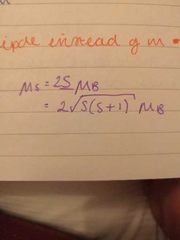
|
|
|
equation for bohr magneton |

|
|
|
resultant magnetic momentum |
precesses around J component of mu R that lies parallel to J gives actual value of dipole moment perpendicular component averages to zero |
|
|
magnetic moment of J |
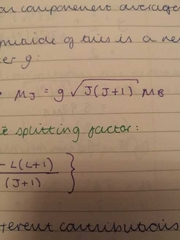
|
|
|
landé splitting factor g |

|
|
|
what are the values of the splitting factor g |
when S=0 g=1 when L=0 g=2 |
|
|
magnetic energy of parallel and antiparallel dipoles |

|
|
|
probability of finding an electron in parallel and antiparallel states |

|
|
|
what happens to probability when thermal energy is larger than the magnetic energy |
probability of parallel is roughly equal to probability of perpendicular magnetic dipole is roughly zero |
|
|
what happens to probability when thermal energy is smaller than magnetic energy |
probability of parallel is larger than probability of perpendicular
|
|
|
brillouin function |

this gives the average dipole component in the field direction as a function it B and T and takes a value between 1 and 0 |
|
|
derive an expression for the magnetic susceptibility in the limit of small. applied fields and high temperatures |

|
|
|
equations for magnetic susceptibility |

|
|
|
bulk properties of a ferromagnetic |
magnetisation is large and positive its contribution to total B field is significant magnetism is a complex function of the applied magnetic H field magnetism depends on history of sample |
|
|
what causes the increasing magnetism in a paramagnet |
increasing alignment of magnetic dipoles |
|
|
how to produce large values of magnetisation in a ferromagnet |
very small H field direct alignment of magnetic dipoles |
|
|
edges of domains |
called walls width of a few 100 atoms wide |
|
|
two main mechanisms by which a ferromagnet is magnetised |
growth of domains with favourably. orientated magnetisation vectors rotation of magnetisation vectors |
|
|
hysteresis effects |
irreversible domain wall motions give rise to these effects |
|
|
domain model for the magnetisation of a ferromagnet |
displacement of domain walls eat away the unfavourable domains whose direction is not aligned with the applied magnetic field |
|
|
what makes a domain wall motion irreversible |
motion of walls is strongly influenced by defects or impurities in the sample |
|
|
the total energy of a ferromagnet crystal has a contribution from 3 mechanisms |
magnetostatic energy
anisotropy energy
exchange energy sum of these must be minimised |
|
|
temperature dependance of a ferromagnet |
if you heat a permanent magnet past the curie temperature and then cool it, it will destroy domain structure |
|
|
sources of an magnetic field |
electric current that flows in a conductor from intrinsic magnetic properties of particles having a spin |
|
|
define H field |
can only be produced by a free current |
|
|
define B field |
related to total current, bound and free |
|
|
what is a magnetic dipole ina in wire |
current times area |
|
|
define magnetisation |
where a non magnetic material is converted to a magnetic material magnetic dipole moment per unit volume |
|
|
relationship of B and H |
B = mu naught H |
|
|
relationship between B and H when there's magnetisation |
B = mu naught (H+M) B = mu naught mu R H |
|
|
2 measures of susceptibility |

|
|
|
force on a conductor in a magnetic field |

|
|
|
circulating negative charge |
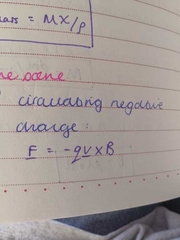
|
|
|
magnetic dipole moment of a circulating electron |

|
|
|
energy when placing a magnetic dipole in a B field |

|
|
|
torque when placing a magnetic dipole in a B field |
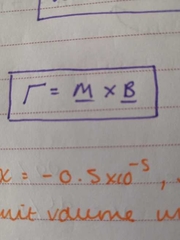
|
|
|
magnetisation and H field |
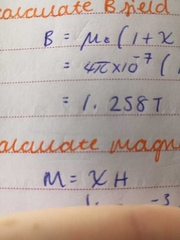
|
|
|
theory of diamagnetism |
all materials are diamagnetic have a small negative values of susceptibility magnetism will oppose an applied magnetic field |
|
|
precession |
the motion of a magnetic dipole in a constant magnetic field |
|
|
precessional motion |

|
|
|
langeins theory of diamagnetism |

|
|
|
what does the precessional motion mean. |

|
|
|
what can cause spontaneous magnetisation |
need alignment of neighbouring magnetic dipoles |
|
|
pauli exclusion principle |
for 2 identical fermions, total wavefunction is antisymmetic under exchange of particles |
|
|
4 ways of writing a wavefunction |
one singlet = spins are antiparallel = symmetric three triplets = spins are parallel = antisymmetic |
|
|
overlap in distributions |
smaller for two electrons in an antisymmetic spatial wavefunction therefore a smaller coulombic repulsion in a triplet wavefunction |
|
|
energy comparison for states |
triplet state is lower than the singlet state |
|
|
energy difference between singlet and triplet |
exchange energy best condition for ferromagnetiv state is when J is positive |

