![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
39 Cards in this Set
- Front
- Back
|
Steps undertaken by CFD solution in 1 time step |
1. Compute fluxes at interfaces 2. Accumulate sum of fluxes for each control volume 3. Update solution given a choice of time step 4. Repeat step 1 |
|
|
Setting up and running CFD solution |
1. Import a mesh - Define control volume 2. Assign physical behaviour - Viscosity, Density, etc 3. Select discretisation scheme - SIMPLE scheme 4. Select numerical accuracy of discretisation - 1st O 5. Impose BCs - Velocity Inlet, Pressure Outlet 6. Impose initial conditions - Uniform flow 7. Define stopping criteria - define residuals 8. Set up monitor for quantities of interest - lift, drag, etc 9. Run simulation until stopping criteria reached 10. Verify if quantities of interest are steady or amend the stopping criteria |
|
|
Mesh quality criteria and its effects |
1. Angle - Skewness less than 120° - May lead to large TE and artificial dissipation 2. Regularity - Structured mesh - Important in areas of high gradient. Hybrid methods lead to full regularity through stacking 3. Smoothness - Stretching is the ratio of consecutive mesh widths. Gradiation necessary for varying flow fields. Stretching needs to be less than 1.1 for high gradients and less than 1.3 for low gradientsa |
|
|
Artificial Viscosity - Definition |
- Scales with jumps between cells. - Required for stability of solution - Considered an error - Proportion to h in 1st O and to h^2 in 2nd O - If too large, mesh needs to be refined until mesh convergence i.e. Further refinement does not change results
|
|
|
Reducing AV |
1. Use small mesh widths in areas of high gradient 2. Use 2nd order scheme, reduces AV by 1/4 3. Maintain good mesh quality in areas of high gradient |
|
|
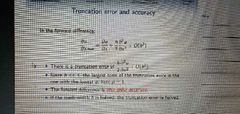
Truncation Error |
- Arises in discrete solution as we are unable to take the limit of h -> 0 - TE vanishes if consistent discretisation used - 1st O - TE proportional to h and for 2nd O - TE proportional to h^2 - In 1st O halving mesh width, halves the TE - In 2nd O halving mesh width, quaters the TE |
|
|
Explicit Time Stepping |
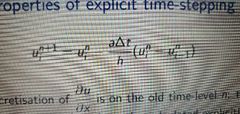
- simple, does not require a matrix to be solved - CFL number has to be less than 1 - small time step needed to be chosen for stability of the scheme |
|
|
Implicit time stepping |

- Requires extra memory to solve a matrix - Not restricted by CFL number - Large time steps can be used for accelerated convergence - Put n + 1 to the space derivative and make u (n i) the subject |
|
|
Temporal Convergence |
- To do with residuals - Removal of unsteadiness from the solution - Quantities of interest need to be monitored to ensure sufficient iterations - Fully converged solution reduces unsteadiness but errors such as TE remains |
|
|
Mesh Convergence |
- To do with TE - Refining mesh until TEs are small enough - Using consistent discretisation (h -> 0) not affordable cannot fully elimitate TE - Insufficient convergence means large errors - A lot of AV - Need to monitor quantities of interest. - Mesh convergence reached when refining mesh won't change these quantities - Modelling Errors still remain |
|
|
Clustering |
- Refining mesh locally in areas of high gradient - Reducing TE - Large gradient - high mesh density, Small gradients - low mesh density - Rate of change of mesh density limited by the smoothness requirement of less than 1.2 in average |
|
|
Obtaining Confidence in CFD results |
- Reducing user errors - Verify if necessary - Ensure adequate convergence - Correct BCs set - Analyse the effect of mesh - Improve mesh quality - Perform mesh refinement study - Compare to experimental data |
|
|
Residual |
- Flux balance of the conservation equations in each cell - RMS of all residuals in each iteration - Used to assess unsteadiness - Cannot drive residuals to zero - Less than 1 x 10^(-6) - Only indicates if quantities of interest have sufficiently converged |
|
|
SIMPLE scheme |
1. Guess pressure field p* 2. Solve momentum equation for velocity field u*, won't be divergence free 3. Solve Pressure correction equation for ∆p 4. if ∆p small enough, time step is complete 5. Correct p* with ∆p 6. Correct u* with the corrected pressure field 7. Go to step 2 |
|
|
Forward Difference |

|
|
|
Backward Difference |

|
|
|
1D advection equation |
Forward time step Backward difference CFL of less than 1 |
|
|
CFL number |
a∆t/h How much the solution has travelled in 1 time step |
|
|
Finite Difference for 1D advection equation |

Advection speed a is taken as a constant |
|
|
Finite Volume - 1D Advection Equation (Flux) |
Flux f equal to au |
|
|
Conservation FDM vs FVM |
FVM is conservative |
|
|
Up winding |
Values taken from left to right |
|
|
FDM Burgers' equation - Non linear advection |

Non conservative |
|
|
FVM Burgers' equation - Non linear advection |

F is a function of u, given in the question. |
|
|
Consistency |
Limit of h taken to 0, if done so TE reduces to zero |
|
|
Order of accuracy, truncation error, etc |
|
|
|
Central difference |

|
|
|
AV - 2nd Order discretisation |

Same with when flux being used |
|
|
1st O and 2nd O FVM - Effect on AV |
1st O - Piece wise constant 2nd O - Piece wise linear Represented as h and h squared respectively |
|
|
Typical boundary conditions in CFD solver |
Velocity inlet Mass flow inlet Pressure inlet Pressure outlet Total pressure inlet Slip or no slip wall Symmetry Periodicity |
|
|
Springs |
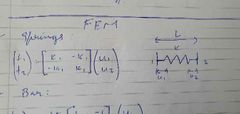
F equals k times x |
|
|
Bar |

|
|
|
Truss |

|
|
|
Potential energy and approximation |

|
|
|
Weighted residual approach |

|
|
|
Finite Volume Method |
Same set up as CFD solution |
|
|
Properties of FDM |
- Only concerned about balancing derivatives - Non conservative |
|
|
BCs Physical example |
Velocity inlet, no slip wall and pressure outlet |
|
|
Non physical BCs example |
Velocity inlet, no slip wall, mass flow outlet |

